Blog

Der erste Teil von Generative Design ermöglichte einen Einblick in die Welt der Parameter und Algorithmen. Dieser Beitrag geht einen Schritt weiter. Für alle die den Anfang verpasst haben <hier> der Link.

Mithilfe der Solver-Funktion wird das parametrische Skript in Gang gesetzt. Einfach gesagt verändert die Solver-Funktion den Wert der Variablen, wodurch verschiedene Varianten erstellt werden. Vergleichbar mit einem Rezept: Mit immer denselben Zutaten lassen sich bei unterschiedlicher Dossierung verschiedene Drinks herstellen. Das Fachwort hierfür lautet Optioneering.

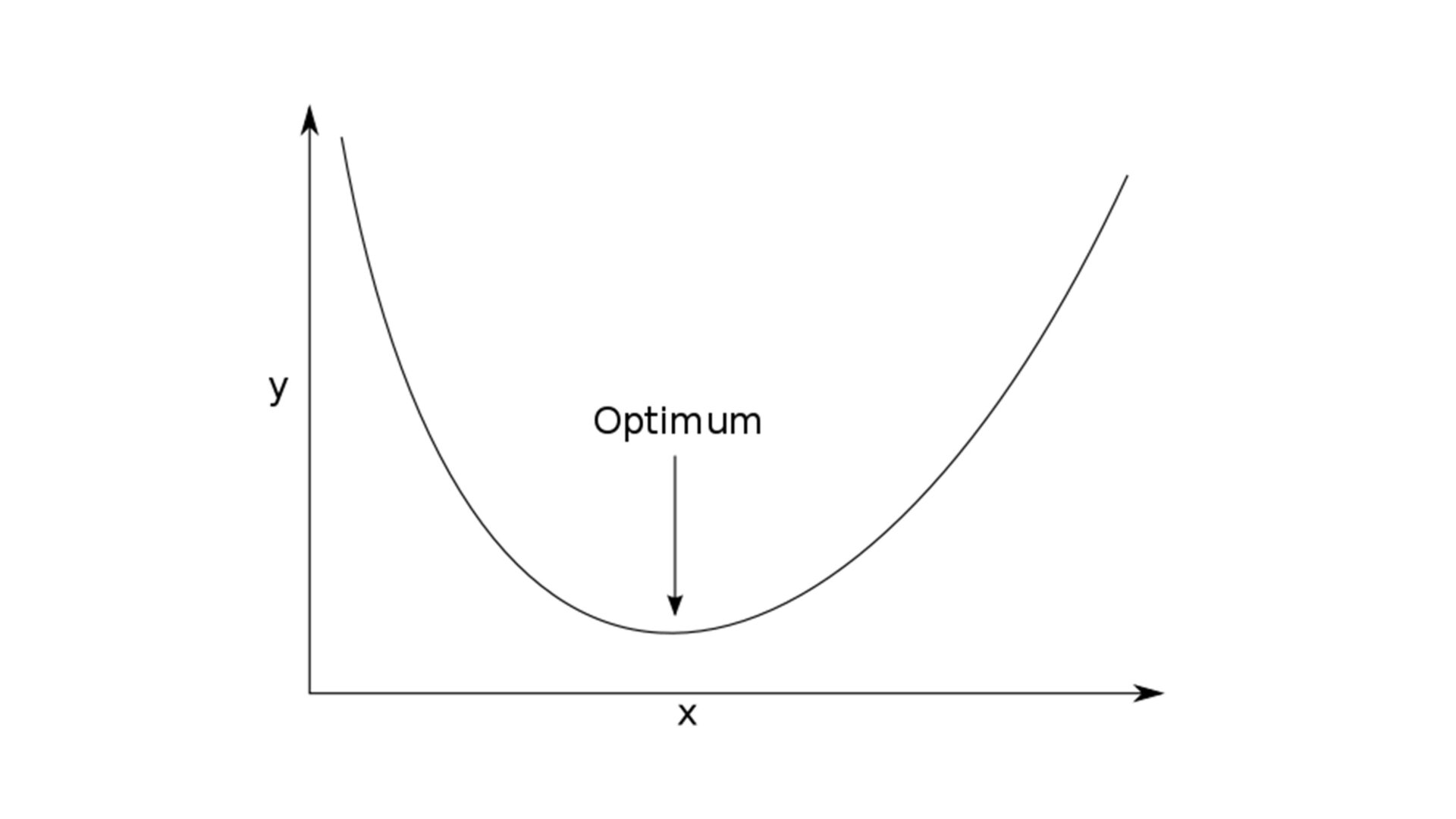
Zwar kann das Erstellen von möglichst vielen Varianten sehr interessant sein, sei es in einem Variantenstudium oder zur Ideenfindung. Interessanter wird es jedoch bei Varianten, die genau unseren Zielen entsprechen. In einer Optimierung passiert genau das. Die Beste Lösung für ein Problem soll gefunden werden.

Mithilfe von objektiven Funktionen kommen die Ergebnisse der «Evaluators» ins Spiel. Es wird festgelegt, welche Werte maximiert und welche Werte minimiert werden sollen. Wurde nur ein einzelnes Ziel festgelegt, ist die Aufgabe einfach. Die Optimierung besteht darin, den bestmöglichen Wert für diesen Parameter zu finden. Wurden jedoch mehrere Ziele festgelegt, wird die Aufgabe schwieriger.

Ein Beispiel für eine Flächenbepflanzung mit Bäumen:

• Die Anzahl der Bäume soll maximiert werden
• Die Kosten für die Bäume sollen minimiert werden
• Die Anzahl grosser Bäume soll maximiert werden

Diese Aufgabe bringt das Problem mit sich, dass keines dieser Ziele zu 100 Prozent erfüllt werden kann, ohne dass eines der anderen Ziele vollkommen verfehlt wird. Die einzige Möglichkeit, dieses Problem zu lösen, ist die Annäherung an das Optimum. In der Welt der Mathematik nennt sich dieses Vorgehen eine “Pareto Optimierung”. Objektive Funktionen besitzen die Fähigkeit, eine “Pareto Optimierung” durchzuführen. Sie wurden so programmiert, die optimalen Ergebnisse zu finden.

Zusammengefasst benötigt eine Optimierung die Daten aus dem parametrischen Skript, Ziele was erreicht werden soll und eine objektive Funktion.

Die beste Variante zu finden ist ein langwieriger Prozess. Theoretisch müsste die objektive Funktion alle möglichen Kombinationen aller Variablen berechnen. Durch die Verwendung von generischen Algorithmen kann dieser Prozess enorm beschleunigt werden.

Generische Algorithmen bedienen sich hierbei am Prinzip der Evolution. Sie werden deshalb auch Evolutionäre Algorithmen (EA) genannt.

In einer ersten Phase werden zufällige Resultate mit dem parametrischen Skript generiert. Dabei sollen möglichst verschiedene Varianten entstehen.

In der zweiten Phase werden diese Varianten durch objektive Funktionen bewertet. Die Resultate werden in der dritten Phase miteinander verglichen und nur die besten Varianten kommen in die nächste Runde.

In der vierten Phase werden die Parameter der Siegervarianten miteinander gekreuzt. Nehmen wir an, wir haben Schildkröten. Die Intelligenz von Schildkröte 1 wird mit der Stärke von Schildkröte 2 gemischt. War Schildkröte 1 sehr intelligent und Schildkröte 2 sehr stark, wird aus dieser Kombination mit grosser Wahrscheinlichkeit eine bessere Schildkröte entstehen.

Die Ergebnisse aus Phase Vier dienen wieder als Input für die Phase Zwei. Je länger dieser Prozess andauert, desto besser wird das Resultat. Wurden jedoch in Phase Eins nur Varianten erstellt, welche ausschliesslich aus schlechten Variablen bestehen, wird nur die beste Variante dieser schlechten Varianten gefunden. Deshalb wird bei jeder Zirkulation nach der Kreuzung eine Mutationsphase hinzugefügt. Zufällig erstellte Varianten werden der Auswahl hinzugefügt und bewertet. War die Auswahl schlecht, wird diese wieder rausgefiltert. War sie gut, fliessen die Variablen in das System.

Zusammengefasst besteht ein generischer Algorithmus aus diesen fünf Phasen:

1. Initialisierung
2. Bewertung
3. Auswahl
4. Kreuzung
5. Mutation

Wie bereits erwähnt setzt die Solver Funktion das Skript in Gang. Es bestehen folgende vier Möglichkeiten, wie das Skript ausgeführt werden kann:

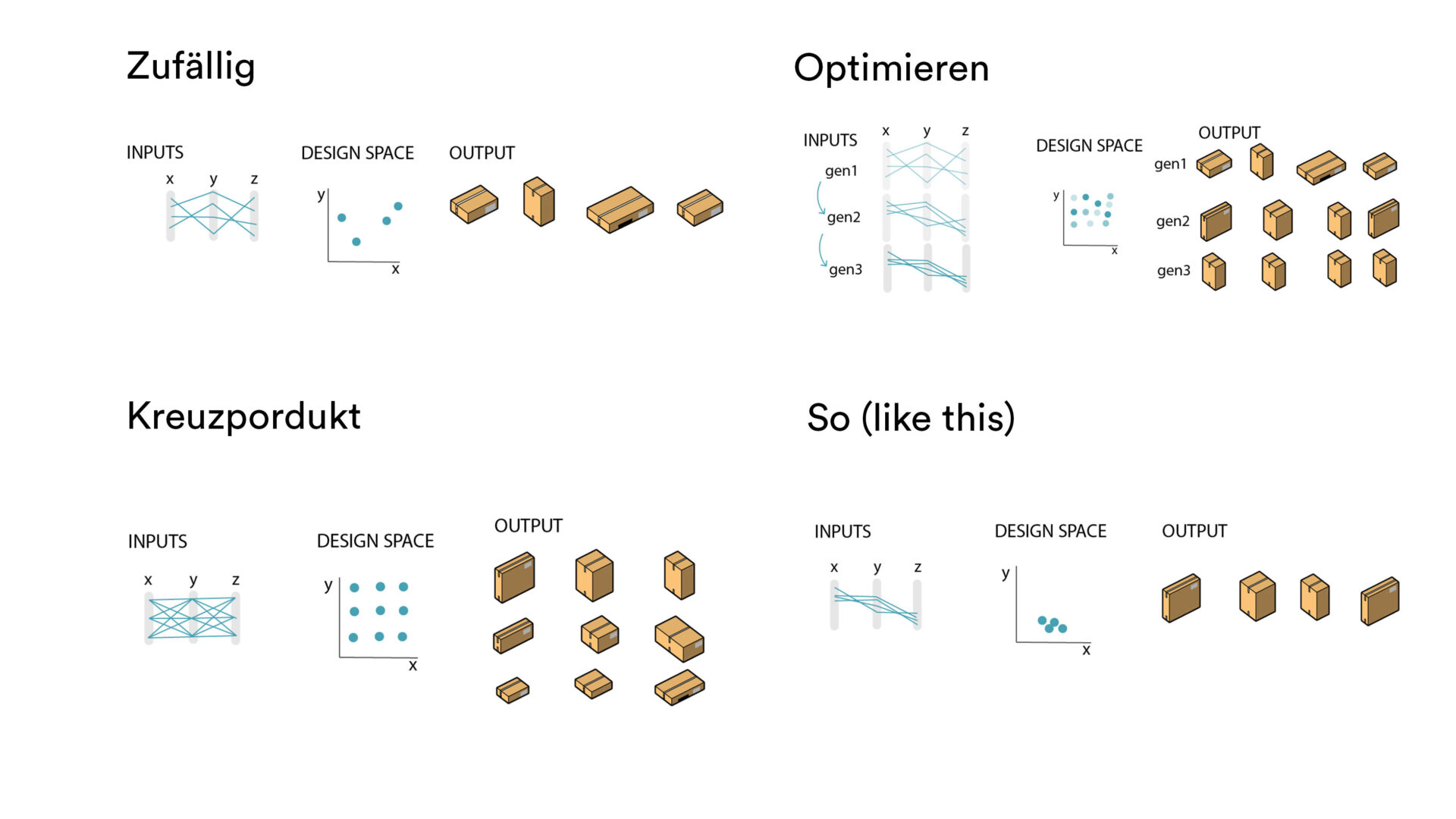
Zufällig

Die Ergebnisse des Solvers sind eine zufällige Auswahl aus den Möglichkeiten des parametrischen Skripts. Die Ergebnisse werden zwar bewertet,haben aber keinerlei Einfluss. Eingabe ist die Anzahl der gewünschten Varianten.

Kreuzprodukt

Die Ergebnisse dieses Solvers sind Varianten, die sich möglichst fest voneinander unterscheiden. Der Algorithmus sucht anhand der objektiven Funktion Varianten, die ein repräsentatives Bild aller möglichen Varianter darstellen. Eingabe ist die Anzahl der gewünschten Varianten.

Optimieren

Durch generische Algorithmen wird das Ergebnis über Generationen verbessert. Der Algorithmus sucht anhand des oben beschriebenen Algorithmus die bestmöglichen Varianten für eine Situation. Eingabe ist die Grösse der Startpopulation und die Anzahl von Generationen.

So

In Englisch heisst dieser Solver «like that» und das trifft den Nagel auf den Kopf. Dem Solver wird ein Resultat mit den entsprechenden Variablen gegeben und der Solver versucht möglichst gleiche Varianten zu erstellen. Eingabe ist die Anzahl der gewünschten Varianten und die Vergleichsvariante.

Wie die Kombination vom parametrischen Skript («Generators» und «Evaluators») mit den «Solver» aussieht, erfahrt ihr im nächsten Beitrag hier anhand eines Generativ Design Skripts zur Verteilung von Bäumen.